Activité 3 - Champ de pesanteur
Contenu de l'activité
Voici le code à exploiter dans l'activité :
#Mesure de g par les oscillations d'un pendule simple
import numpy as np
import matplotlib.pyplot as plt
from math import *
##################################################################
########################Données à modifier########################
##################################################################
l = np.array([0.1,0.2,0.3,0.4,0.5])
T = np.array([1,2,3,4,5])
##################################################################
##################################################################
N = len(T)
#Calcul de T2
T2 = []
for i in range (0,N):
T2.append(T[i]*T[i]/(4*pi*pi))
#Définition de la régression linéaire, on utilise le modèle ax + b afin de vérifier que b est bien proche de 0
parametres=np.polyfit(T2,l,1)
a=parametres[0]
b=parametres[1]
print("a={:.3f}\nb={:.3f}".format(a,b))
plt.plot(T2,l,'xr',label="Données expérimentales")
plt.plot([T2[0],T2[-1]],[a*T2[0]+b,a*T2[-1]+b],'-b',label="Régression linéaire")
plt.ylabel("Longueur du fil en m")
plt.xlabel("(T/2pi)^^2 en s^^2")
plt.legend()
plt.grid()
plt.show()
#Calcul de g pour chaque couple de valeur (l, T2)
g_cal = []
for i in range (0,N):
g_cal.append(l[i]/T2[i])
#Calcul de l'écart type pour g
s = np.std(g_cal)
#Calcul de l'incertitude pour g
u_g=s/sqrt(N)
print("g={:.3f} N/kg \n u_g={:.3f} n/kg".format(a,u_g))
Vidéos de cours⚓︎
Il s'agit d'une vidéo rapide qui prend appuie sur l'exemple d'un exercice.
Si vous souhaitez une vidéo plus complète, celle-ci dure 12min (vous ne tiendrez compte que des interactions gravitationnelles et électrostatiques) :
Cours⚓︎
Champ de pesanteur et de gravitation⚓︎
Tout corps possédant une masse crée autour de lui un champ vectoriel de gravitation. Quand ce champ est crée à la surface d'une planète, on parle de champ de pesanteur.
Lignes de champ⚓︎
Ce sont des courbes orientées qui traduisent les caractéristiques d’un champ vectoriel dans une zone de l’espace. Dans les champs gravitationnels, ce sont des lignes orientées vers le centre du corps qui crée le champ de gravitation.

Expressions vectorielles⚓︎
Pour écrire le champ de gravitation perçu par un corps B (de masse \(m_B\)) distant (de la distance \(d\)) du corps A (de masse \(m_A\)), on aura : \(\vec G = {\vec F_{A/B} \over m_B}=G \times {m_A \over d^2} \times \vec u_{BA}\)
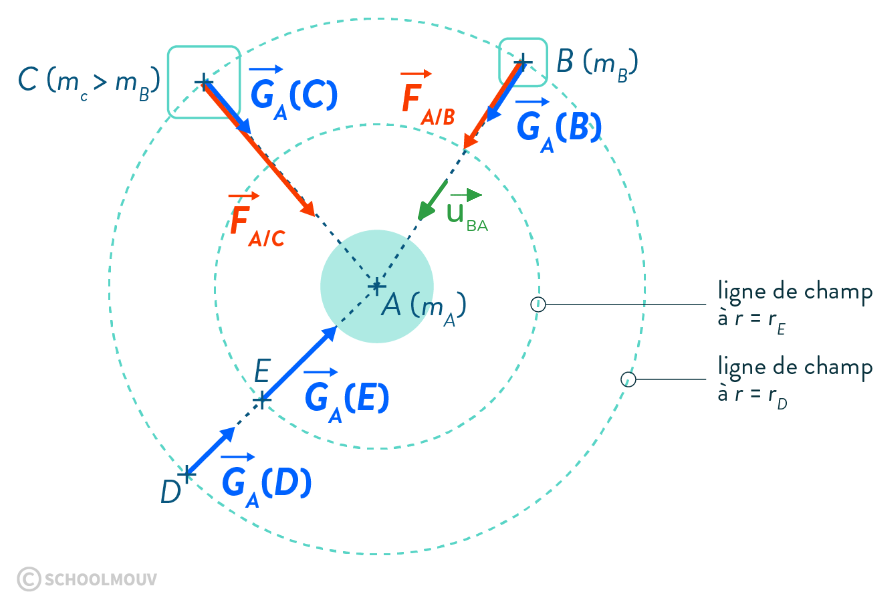
Pour un champ de pesanteur perçu par un corps de masse \(m\), on aurait : \(\vec P = m \times \vec g\).
Champ électrostatique⚓︎
Tout corps possédant une charge électrique crée autour de lui un champ vectoriel électrostatique. L'orientation de ce champ dépendra du signe de la charge étudiée.
Lignes de champ⚓︎
Dans les champs électrostatiques, ce sont des lignes orientées :
- du centre vers l'extérieur du corps qui crée le champ si sa charge est positive.
- vers le centre du corps qui crée le champ si sa charge est négative.
Expressions vectorielles⚓︎
Pour écrire le champ électrostatique perçu par un corps B (de charge \(q_B\)) distant (de la distance \(d\)) du corps A (de charge \(q_A\)), on aura : \(\vec E = {\vec F_{A/B} \over q_B}=k \times {q_A \over d^2} \times \vec u_{BA}\)

On remarque alors que la force électrostatique dépend de la charge qui subit la force mais aussi de l'orientation du champ.
