Voici deux animations qui viendront compléter les documents mis à disposition dans l'activité du manuel.
Cours rédigé
Forces et champs⚓︎
Au préalable⚓︎
Les situations étudiées ici se feront entre deux corps A (\(m_A\) et \(q_A\)) et B (\(m_B\) et \(q_B\)).
Il conviendra de définir un vecteur unitaire entre les centres de ces deux corps pour définir les expressions vectorielles des forces et des champs.
Force de gravitation⚓︎
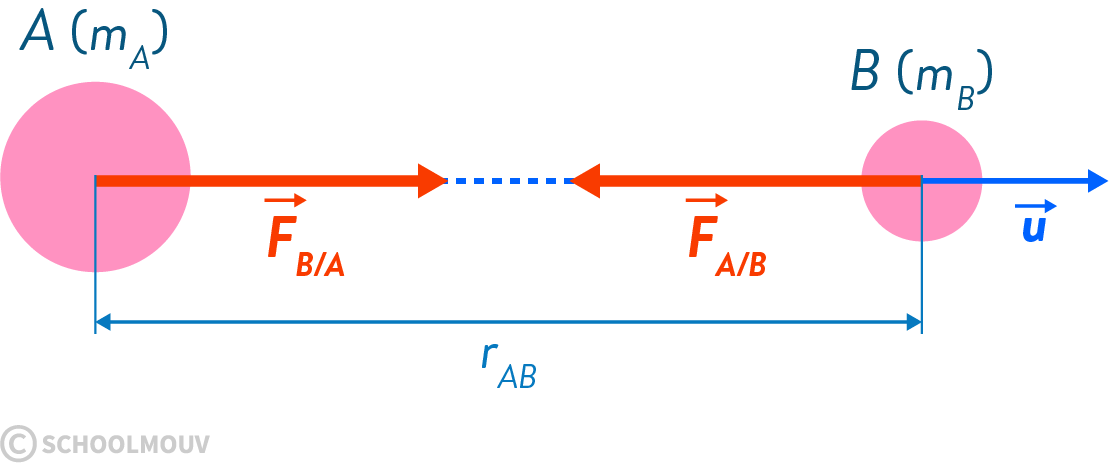
La force de gravitation sera une action toujours attractive.
Données et unités⚓︎
- Constante de gravitation universelle : \(G = 6,67 \times 10^-11 N \cdot m^2 \cdot kg^{-2}\);
- Masses (\(m_A\) et \(m_B\)) : en kg ;
- Distance : en m ;
- Force : en N.
Expressions vectorielles⚓︎
- \(\vec F_{A/B} = - G \times {m_A \cdot m_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = G \times {m_A \cdot m_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = - \vec F_{A/B}\)
Calcul de norme⚓︎
La norme d'un vecteur force correspond à la valeur de cette force en N.
\(F_{A/B}=F_{B/A} = G \times {m_A \cdot m_B \over r_{AB}^2}\)
Force électrostatique⚓︎
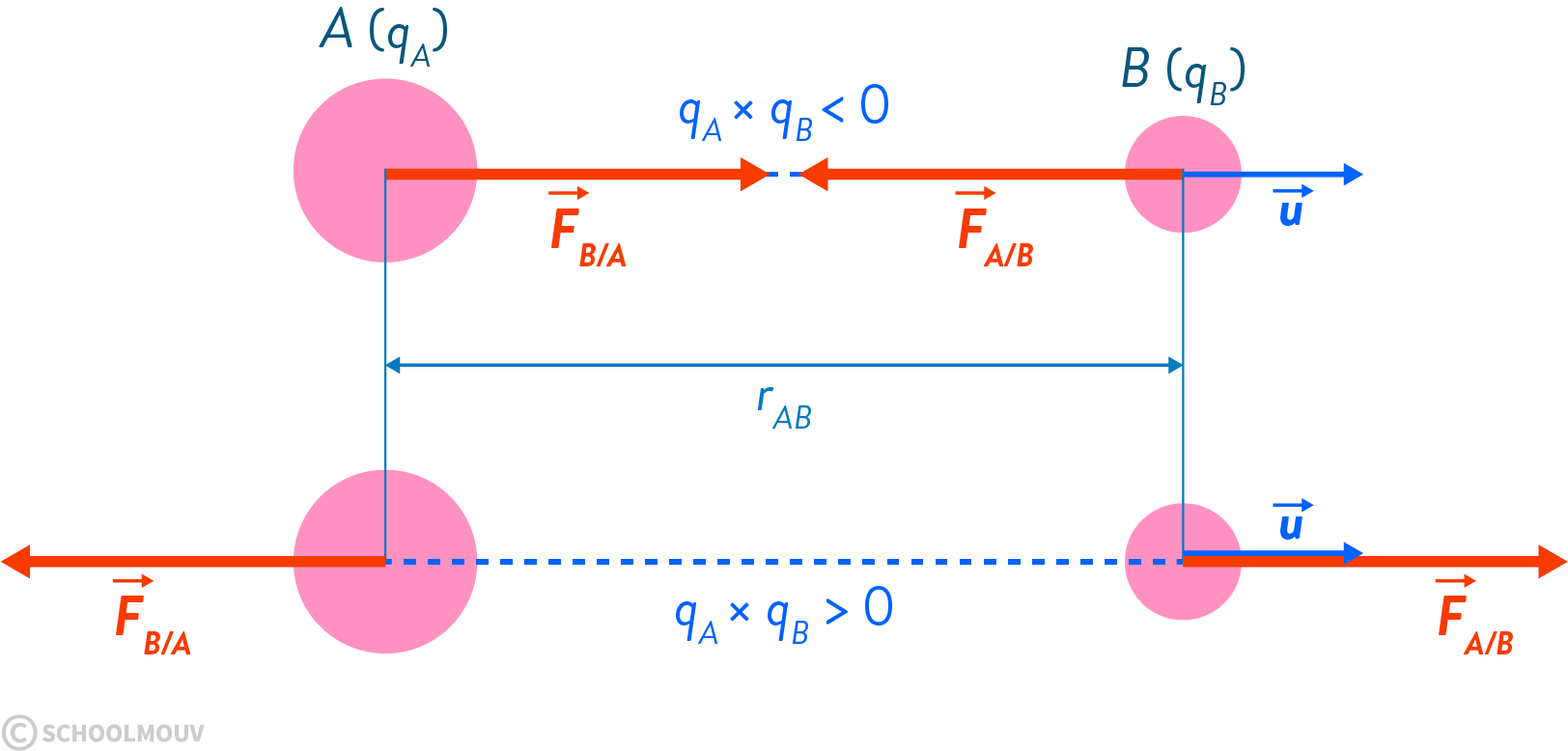
La force électrostatique sera considérée attractive ou répulsive en fonction des charges mises en jeu dans l'étude considérée.
Données et unités⚓︎
- Constante de Coulomb : \(k = {1 \over 4 \pi \epsilon_0} = 8,99 \times 10^9 N \cdot m^2 \cdot C^{-2}\);
- Charges (\(q_A\) et \(q_B\)) : en C ;
- Distance : en m ;
- Force : en N.
Expressions vectorielles⚓︎
Cas où \(q_A\times q_B < 0\) :⚓︎
- \(\vec F_{A/B} = - k \times {q_A \cdot q_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = k \times {q_A \cdot q_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = - \vec F_{A/B}\)
Cas où \(q_A\times q_B > 0\) :⚓︎
- \(\vec F_{A/B} = k \times {q_A \cdot q_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = -k \times {q_A \cdot q_B \over r_{AB}^2} \vec u\)
- \(\vec F_{B/A} = - \vec F_{A/B}\)
Calcul de norme⚓︎
La norme d'un vecteur force correspond à la valeur de cette force en N.
\(F_{A/B}=F_{B/A} = k \times {{|q_A \cdot q_B|}\over r_{AB}^2}\)